I recently gave a talk at the Solving Polynomial Systems seminar about Linear Convex Optimization and the Gurobi software (here part of the material presented). Gurobi is a state-of-the-art optimization software. It offers a free academic license; for people outside the academia open alternatives like GLPK are available. In this short series of post I will showcase different usages of this powerful software to solve different problems. Most of the ideas presented here are inspired on the lectures of Prof. Gualandi, which can be found in this repo.
The source code for this example can be found here: sudoku.py
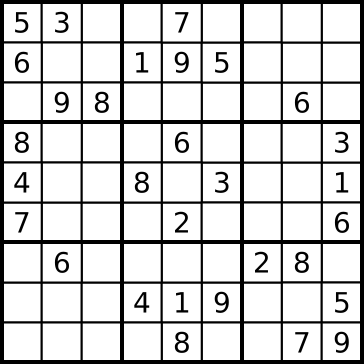
In the first example we will see how to formulate and solve a sudoku as an Integer Linear Programming (ILP) problem. A standard sudoku is a $9\times9$ grid which must be filled with the numbers from $1$ to $9$, such that each number appear only once in each row, column and subgrid. Here is an example:
A sudoku can be easily formulated as ILP problem. Notice that in this case we are not interested in optimizing some function; we only need a feasible solution. This kind of problems, which are equivalent to optimizing a linear function, are called feasibility problems.
First of all, we represent a sudoku as a text string with 9 rows, each one representing a grid row; cells are separated by a space character, and empty cells are represented by a dot. This representation allows us to read it easily. The above grid becomes the following:
1
2
3
4
5
6
7
8
9
10
sudoku = """5 3 . . 7 . . . .
6 . . 1 9 5 . . .
. 9 8 . . . . 6 .
8 . . . 6 . . . 3
4 . . 8 . 3 . . 1
7 . . . 2 . . . 6
. 6 . . . . 2 8 .
. . . 4 1 9 . . 5
. . . . 8 . . 7 9"""
grid = [row.strip().split(' ') for row in sudoku.split("\n")]
Now we want to extract our ILP instance from the grid. To do so, we define $9^3$ binary variables $x_{ijk}$, with $1 \leq i,j,k \leq 9$. In the final solution, we want $x_{ijk}=1$ if and only if the cell $(i,j)$ of the grid (i-th row and j-th column) contains the value $k$. We can do that very easily using gurobipy, the python library of Gurobi:
1
2
3
4
5
6
import gurobipy as gp
from gurobipy import GRB
model = gp.Model('sudoku')
vars = model.addVars(n, n, n, vtype=GRB.BINARY, name='G')
The first family of constraints that we want to impose on our instance are the grid constraints: we want to force $x_{ijk}=1$ for each cell $(i,j)$ in the starting grid whose value is $k$. We do it by setting vars.LB = 1 for the right variables; this is enough since vars contains only binary variables.
1
2
3
4
5
for i in range(n):
for j in range(n):
if grid[i][j] != '.':
v = int(grid[i][j]) - 1
vars[i, j, v].LB = 1
The second family are the cell constraints: each cell can contain only one value. This means that for each fixed $i$ and $j$, we want only one $x_{ijk}$ to be equal to one. For binary variables, this is equivalent to require that for each fixed $i,j$,
\[\sum_k x_{ijk} = 1,\]which results in the following code
1
2
3
4
model.addConstrs(
(vars.sum(i, j, '*') == 1
for i in range(n)
for j in range(n)), name='V');
Similarly, we want to impose the row constraints (each number can appear only once per row) and the column constraints. The row constraints can be imposed requiring that for each row $i$ and each number $j$ the number of nonzero $x_{ijk}$ (or equivalently the sum over $j$ of $x_{ijk}$) is equal to one. The same holds for the column constraints with the sum over $i$.
1
2
3
4
5
6
7
8
9
10
11
# Each value appears once per row
model.addConstrs(
(vars.sum(i, '*', k) == 1
for i in range(n)
for k in range(n)), name='R');
# Each value appears once per column
model.addConstrs(
(vars.sum('*', j, k) == 1
for j in range(n)
for k in range(n)), name='C');
The last family are the subgrid constraints. This ones are a bit trickier, but not so much: we ask that for each fixed number $k$, the sum of the $x_{ijk}$ over all $i$ and $j$ belonging to a subgrid is $1$.
1
2
3
4
5
6
7
s = 3 # sub-grid size
model.addConstrs((
gp.quicksum(vars[i, j, k] for i in range(i0*s, (i0+1)*s)
for j in range(j0*s, (j0+1)*s)) == 1
for k in range(n)
for i0 in range(s)
for j0 in range(s)), name='Sub');
Finally, we ask Gurobi to optimize our model; this is equivalent to simply solving it, since we gave no objective function.
1
2
3
4
5
6
7
8
9
10
solution = model.getAttr('X', vars)
sol = ''
for i in range(n):
for j in range(n):
for v in range(n):
if solution[i, j, v] > 0.5:
sol += str(v+1) + ' '
sol += '\n'
print(sol)
This give us very quickly the final solution:
1
2
3
4
5
6
7
8
9
5 3 4 6 7 8 9 1 2
6 7 2 1 9 5 3 4 8
1 9 8 3 4 2 5 6 7
8 5 9 7 6 1 4 2 3
4 2 6 8 5 3 7 9 1
7 1 3 9 2 4 8 5 6
9 6 1 5 3 7 2 8 4
2 8 7 4 1 9 6 3 5
3 4 5 2 8 6 1 7 9
Notice that, as often happens with LP models, the main strength of this method is its flexibility. Only changing a couple of lines this script can easily be adapted to larger sudoku (like $16\times 16$ or more) or versions with additional rules (killer-sudoku, hypersudoku…). On the other hand, ad-hoc heuristics may be faster in theory. However, due to the high level performance of the Gurobi software, this is usually not a problem.